Theory Of Computation
Automata – What is it?
Automata theory (also known as Theory Of Computation) is a theoretical branch of Computer Science and Mathematics, which mainly deals with the logic of computation with respect to simple machines, referred to as automata.
Automata* enables scientists to understand how machines compute the functions and solve problems. The main motivation behind developing Automata Theory was to develop methods to describe and analyze the dynamic behavior of discrete systems.
Automata originated from the word “Automaton” which is closely related to “Automation”.
An automaton with a finite number of states is called a Finite Automaton (FA) or Finite State Machine (FSM).
Related Terminologies
Symbols:
Symbols are an entity or individual objects(smallest possible), which can be any letter, alphabet or any picture.
Example:
1, a, b, #
Alphabet
Definition − An alphabet is any finite set of symbols.It is denoted by ∑.
Example − ∑ = {a, b, c, d} is an alphabet set where ‘a’, ‘b’, ‘c’, and ‘d’ are symbols.
Examples:
- ∑ = {a, b}
- ∑ = {A, B, C, D}
- ∑ = {0, 1, 2}
- ∑ = {0, 1, ....., 5]
- ∑ = {#, β, Δ}
- ∑ = {a, b}
String
Definition − A string is a finite sequence of symbols taken from ∑.
Example − ‘cabcad’ is a valid string on the alphabet set ∑ = {a, b, c, d}
Length of a String
Definition − It is the number of symbols present in a string. (Denoted by |S|).
Examples −
If S = ‘cabcad’, |S|= 6
If |S|= 0, it is called an empty string (Denoted by λ or ε)
Kleene Star
Definition − The Kleene star, ∑*, is a unary operator on a set of symbols or strings, ∑, that gives the infinite set of all possible strings of all possible lengths over ∑ including λ.
Representation − ∑* = ∑0 ∪ ∑1 ∪ ∑2 ∪……. where ∑p is the set of all possible strings of length p.
Example − If ∑ = {a, b}, ∑* = {λ, a, b, aa, ab, ba, bb,………..}
Kleene Closure / Plus
Definition − The set ∑+ is the infinite set of all possible strings of all possible lengths over ∑ excluding λ.
Representation − ∑+ = ∑1 ∪ ∑2 ∪ ∑3 ∪…….
∑+ = ∑* − { λ }
Example − If ∑ = { a, b } , ∑+ = { a, b, aa, ab, ba, bb,………..}
Language
Definition − A language is a subset of ∑* for some alphabet ∑. It can be finite or infinite.
Example − If the language takes all possible strings of length 2 over ∑ = {a, b}, then L = { ab, aa, ba, bb }
Example: Finite Language
L1 = {Set of string of length 2}
= {aa, bb, ba, bb}
Example: Infinite Language
L2 = {Set of all strings starts with 'a'}
= {a, aa, aaa, abb, abbb, ababb,.....}
Formal definition of a Finite Automaton
An automaton can be represented by a 5-tuple (Q, ∑, δ, q0, F), where −
Q is a finite set of states.
∑ is a finite set of symbols, called the alphabet of the automaton.
δ is the transition function.
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).
Formal Notation used in the representation of Finite Automata
We can represent Finite automata in two ways, which are given below:
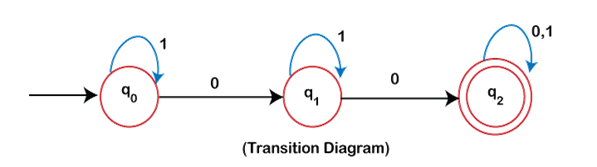
- Transition diagram
The transition diagram is also called a transition graph; it is represented by a diagraph. A transition graph consists of three things:
- Arrow (->): The initial state in the transition diagram is marked with an arrow.
- Circle : Each circle represents the state.
- Double circle : Double circle indicates the final state or accepting state.
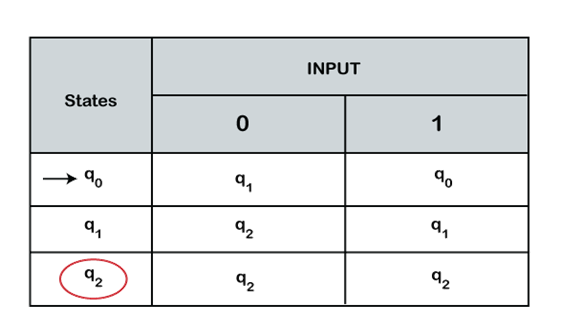
- Transition Table
It is the tabular representation of the behavior of the transition function that takes two arguments, the first is a state, and the other is input, and it returns a value, which is the new state of the automata. It represents all the moves of finite-state function based on the current state and input. In the transition table, the initial state is represented with an arrow, and the final state is represented by a single circle. Formally a transition table is a 2-dimensional array, which consists of rows and columns where:
- The rows in the transition table represent the states.
- The columns contain the state in which the machine will move on the input alphabet.
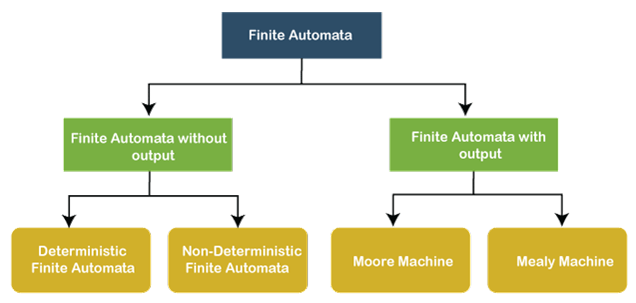
Types of Finite Automata
Examples:
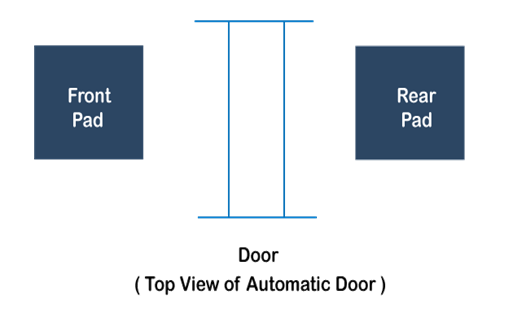
The example of Finite state Automata is Automatic door controller because it has limited memory for detecting the present state of the controller, automatic doors are often found at entrance and exists of various hotels, supermarkets, theaters and hospitals etc. Automatic door have two pads that are used for detection:
Front Pad: This is located at front of the doorway to detect the presence of the person.
Rear Pad: This pad is located at backside of the doorway. In this, controller hold the door to open till the person passes all the way through it.
Some other examples of finite automata are elevator, digital watches, dish washes and calculators.
Important features of Finite Automata
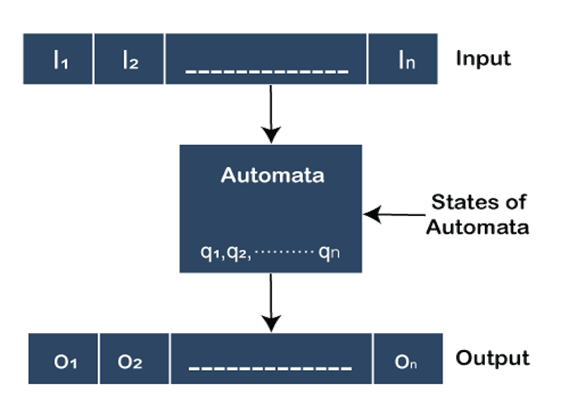
Input: Finite Automata takes some input and with the use of this input we can produce some output. The input of the automata is given in the input tape used in the automata. This tape is divided into cells or squares which can hold one symbol at a time.
Output: Finite Automata produce some output with the use of some input.
States of Automata: Automata have finite number of input states. States of Automata like q0, q1…qn.
State Relation: State relations show how automata moves from one state to another state. The next state of the automata at any instant of time is determined by the present state and the input.
Advantages of finite Automata
Below are some advantages of Finite State Automata and Finite State Machine:
- Finite state machines are very flexible.
- Well suited for domains where execution time is shared between various modules.
- In finite state automata, we can easily determine the reachability of an input state whether it is accepted or rejected.
Disadvantages of finite Automata
Below are some disadvantages of Finite State Automata and Finite State Machine:
- Finite state Automata have very limited amount of memory.
- Various multiplications operations on large numbers cannot be carried out on finite automata, because it has limited memory and it cannot remember the full-length sequence of large numbers.
- Not applicable for all types of applications.
- Finite state Automata cannot process Natural Language processes.
- Finite state automata have less computational power than some other models of computation used in automata such as Push down Automata, linear bounded automata and Turing machine.
Applications of Finite Automata
Finite Automata is used in various fields like science, mathematics, and engineering. Below are some applications of finite automata:
Finite state Automata used in Word Processor Programs to provide features, which allow us to search for a given string.
- It is used in Digital Logic Design to control units for a disk or an Input/output controller on a process.
- It is used in Lexical Analysis phase in complier design.
- It is used in various spell checker applications.
- It is used in various Circuit switching design.
- It is used in various text editors.
Deterministic Finite Automaton
Finite Automaton can be classified into two types −
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NDFA / NFA)
Deterministic Finite Automaton (DFA)
In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.
Formal Definition of a DFA
A DFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where −
Q is a finite set of states.
∑ is a finite set of symbols called the alphabet.
δ is the transition function where δ: Q × ∑ → Q
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).
Graphical Representation of a DFA
A DFA is represented by digraphs called state diagram.
- The vertices represent the states.
- The arcs labeled with an input alphabet show the transitions.
- The initial state is denoted by an empty single incoming arc.
- The final state is indicated by double circles.
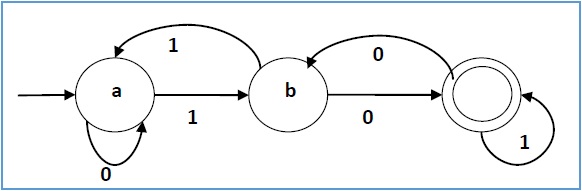
Example
Let a deterministic finite automaton be →
- Q = {a, b, c},
- ∑ = {0, 1},
- q0 = {a},
- F = {c},
Transition function δ as shown by the following table −
| Present State |
Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
Its graphical representation would be as follows −
Non-deterministic Finite Automaton
In NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine. In other words, the exact state to which the machine moves cannot be determined. Hence, it is called Non-deterministic Automaton. As it has finite number of states, the machine is called Non-deterministic Finite Machine or Non-deterministic Finite Automaton.
Formal Definition of an NDFA
An NDFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where −
Q is a finite set of states.
∑ is a finite set of symbols called the alphabets.
δ is the transition function where δ: Q × ∑ → 2Q
(Here the power set of Q (2Q) has been taken because in case of NDFA, from a state, transition can occur to any combination of Q states)
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).
Graphical Representation of an NDFA: (same as DFA)
An NDFA is represented by digraphs called state diagram.
- The vertices represent the states.
- The arcs labeled with an input alphabet show the transitions.
- The initial state is denoted by an empty single incoming arc.
- The final state is indicated by double circles.
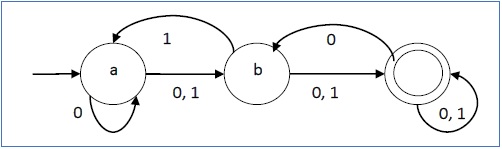
Example
Let a non-deterministic finite automaton be →
- Q = {a, b, c}
- ∑ = {0, 1}
- q0 = {a}
- F = {c}
The transition function δ as shown below −
| Present State | Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| a | a, b | b |
| b | c | a, c |
| c | b, c | c |
Its graphical representation would be as follows −
DFA vs NDFA
The following table lists the differences between DFA and NDFA.
| DFA | NDFA |
|---|---|
| The transition from a state is to a single particular next state for each input symbol. Hence it is called deterministic. | The transition from a state can be to multiple next states for each input symbol. Hence it is called non-deterministic. |
| Empty string transitions are not seen in DFA. | NDFA permits empty string transitions. |
| Backtracking is allowed in DFA | In NDFA, backtracking is not always possible. |
| Requires more space. | Requires less space. |
| A string is accepted by a DFA, if it transits to a final state. | A string is accepted by a NDFA, if at least one of all possible transitions ends in a final state. |
Comments
Post a Comment